Ocena ryzyka metodą Iterum 21.5

Przepisy nakazujące przeprowadzanie oceny ryzyka, pozostawiają pełną dowolność w doborze metody tej oceny. Szukamy takiej, która będzie prosta i spójna z wymaganiami norm zharmonizowanych z dyrektywą maszynową.

Wprowadzenie

Norma ISO 13849-1, definiująca pojęcie poziomu niezawodności (performance level, PL) funkcji bezpieczeństwa, definiuje PL jako prawdopodobieństwo niebezpiecznego uszkodzenia oraz proponuje¹⁾załącznik A ma status „informacyjny“, nie „normatywny“ prosty graf do określania wymaganego poziomu niezawodności (PLr, required PL).

Zakresy prawdopodobieństwa (PFHd²⁾average probability of dangerous failure per hour, średnie prawdopodobieństwo uszkodzenia niebezpiecznego na godzinę) określone dla poszczególnych poziomów:

PL	zakres
a	10⁻⁴ > PFHd ⩾ 10⁻⁵
b	10⁻⁵ > PFHd ⩾ 3×10⁻⁶
c	3×10⁻⁶ > PFHd ⩾ 10⁻⁶
d	10⁻⁶ > PFHd ⩾ 10⁻⁷
e	10⁻⁷ > PFHd ⩾ 10⁻⁸

Tabela powyższa stanie się czytelniejsza, gdy uwzględnimy same wykładniki, tzn. gdy wartości PFHd zmienimy na ich logarytm dziesiętny.

PL	log(PFHd)(sup)3)supremum (sup) i infimum (inf) różnią się od maximum (max) i minimum (min) tym, że nie należą do ograniczanego przedziału	log(PFHd)(min)	ρ(inf)	ρ(max)	lata(inf)4)rok liczy ok. 8766 godzin, więc 0,0001/PFHd odpowiada w przybliżeniu ilości lat, które statystycznie powinny upłynąć bez awarii
a	-4	-5	0	1	1
b	-5	-5,55)ok. -5,523	1	1,5	10
c	-5,5	-6	1,5	2	30
d	-6	-7	2	3	100
e	-7	-8	3	4	1000

PL i ρ mogą być użyte jako wskaźniki poziomu ryzyka — wiadomo, im większe ryzyko, tym staranniej musimy się przed nim zabezpieczyć.

Wspomniany graf, służący do wyboru właściwego PL (a więc i do określenia poziomu ryzyka), można przedstawić w formie tabelarycznej.

S	F	P	PLr
S1	F1	P1	a
S1	F1	P2	b
S1	F2	P1	b
S1	F2	P2	c
S2	F1	P1	c
S2	F1	P2	d
S2	F2	P1	d
S2	F2	P2	e

Łatwo zauważyć, że kombinacje (F1, P2) i (F2, P1) dają zawsze te same wyniki (PL b, PL d). Oznaczmy kombinację (F, P) przez φ i przypiszmy jej wartości liczbowe: φ=0 dla (F1, P1), φ=0,5 dla (F1, P2) i (F2, P1), φ=1 dla (F2, P2). Oznaczmy też przez σ reprezentację liczbową S: σ=0 dla S1 i σ=1 dla S2. Powyższa tabela przyjmie dzięki tym oznaczeniom prostszą postać, którą można uzupełnić wartościami ρ określonymi wcześniej.

σ	φ	PLr	ρ(inf)	ρ(max)
0	0	a	0	1
0	0,5	b	1	1,5
0	1	c	1,5	2
1	0	c	2	2
1	0,5	d	2	3
1	1	e	3	4

Szukamy analitycznej funkcji,⁶⁾ℝ² → ℝ która będzie zarazem dobrym przybliżeniem wartości podanych w tabeli i pozwoli na ekstrapolację poza wyznaczony tymi wartościami zakres.

ekstrapolacja

Zakresy określone w ISO 13849-1 dla S i F są niewystarczające dla potrzeb oceny ryzyka.

Po pierwsze, S1 to „skutki odwracalne“, czyli np. złamania, przecięcia, oparzenia. Potrzebny jest jeszcze jakiś poziom „S0“, gdy konstrukcja jest bezpieczna wewnętrznie lub potencjalne skutki są praktycznie pomijalne (drobne skaleczenia, stłuczenia, oparzenia I stopnia).

Po drugie, gdy zastosujemy techniczne środki ochronne, prawdopodobieństwo zdarzenia spadnie znacznie poniżej F1, określonego jako „nie częściej niż raz na 15 minut“. Dla porównania — najniższy poziom niezawodności (PL a) dopuszcza niebezpieczne uszkodzenie rzadziej niż raz na rok.

Po trzecie wreszcie, same poziomy niezawodności, czyli miara ryzyka, wymagają wprowadzenia dodatkowej wartości „PL 0“ do opisu sytuacji, gdy nawet PL a nie jest konieczne.

pułapki dokładności

Dwa liniowe ciągi wartości ρ: (1, 1,5, 2) dla σ=0 oraz (2, 3, 4) dla σ=1 kuszą, by wyznaczyć powierzchnię wytyczoną przez dwie określone w ten sposób proste, np.:

ρ = (1 + φ) / (1 – σ/2).

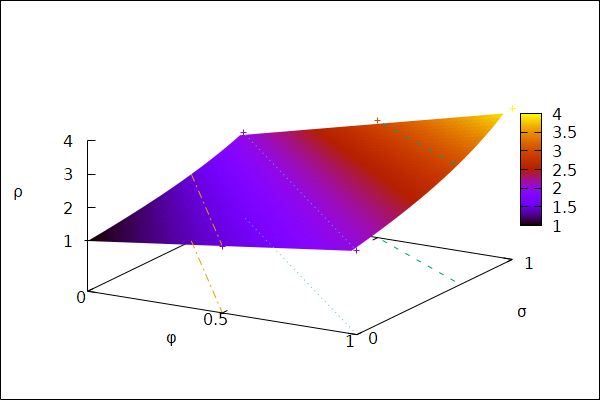
Powierzchnia ta ma tę zaletę, że przechodzi dokładnie przez wszystkie punkty (σ, φ, ρ), wskazane w powyższej tabeli, pojawia się jednak osobliwość dla σ = 2. Jest to, co prawda, daleko poza zakresem rzeczywistych wartości σ,⁷⁾wartość maksymalna, tzn. S2, to σ=1 ale wygląda podejrzanie. Ponadto byłyby problemy z ekstrapolacją — przy znacznym zmniejszeniu częstości (φ < -1) funkcja przyjmuje wartości poniżej zera.⁸⁾liczby ujemne nie są niczym złym, ale „ujemne ryzyko“ rani nasze przyzwyczajenia

Jeśli jednak zgodzimy się na drobne odchylenia od wartości tabelarycznych, możemy je przybliżyć zależnością:

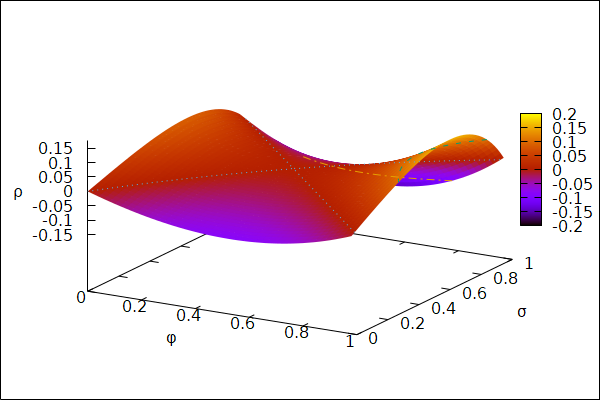
ρ = 2^{σ + φ}.

W przeciwieństwie do poprzedniej, funkcja wykładnicza jest bardzo regularna. Czy ktoś dostrzega różnice wartości? W omawianym obszarze nie przekraczają ±0,2.

szlifowanie

Przyjmijmy kilka oznaczeń:

S := 2σ + 1,⁹⁾tzn. S1=1, S2=3

R := S + F + P,

gdzie F1 = 1, F2 = 2, P1 = 0, P2 = 1, tzn.:

F + P = 2φ + 1.

Wówczas:

R = 2 + 2 (σ + φ) = 2 + 2 log₂(ρ) = 2 + 2 log₂(-log(PFHd) – 4).¹⁰⁾tzn. PFHd = 10^{-4 – ρ},
ρ = 2^{R/2 – 1}

Tabela wiążąca S, F, P, ryzyko R i PLr przybierze postać:

S	F	P	R(max) = S+F+P	R(inf) = R(max)-1	PLr
1	1	0	2	1	a
1	1	1	3	2	b
1	2	0	3	2	b
1	2	1	4	3	c
3	1	0	4	3	c
3	1	1	5	4	d
3	2	0	5	4	d
3	2	1	6	5	e

Wyjaśnić jeszcze należy wartość R_(inf) = 1 dla PLr a, co odpowiada wartości PFHd ≈ 2×10⁻⁵. Zgodnie z normą, powinna się tu znaleźć wartość -∞, odpowiadająca PFHd = 10⁻⁴. Godząc się na to odstępstwo, zyskujemy regularność:

R_(inf) = R_(max) – 1

oraz możliwość traktowania R ⩽ 1 jako ryzyka akceptowalnego.

zmniejszanie ryzyka

Ogólną zasadą przy szacowaniu zagrożeń jest szacowanie z góry. Wyznaczając wartość określającą ryzyko pierwotne,¹¹⁾inaczej: ryzyko wyjściowe, tzn. ryzyko przed zastosowaniem środków ochronnych bierzemy więc pod uwagę:

Rr = R_(max) = S + F + P.

Na tej samej (ostrożnej) zasadzie przyjmujemy, że funkcje ochronne zrealizowane na określonym poziomie niezawodności, obniżają prawdopodobieństwo zdarzenia niebezpiecznego o wartość najmniejszą możliwą dla danego PL:

A = R_(inf).¹²⁾jeśli PFHd jest znane, A = 2 + 2 log₂(-log(PFHd) – 4)

W wyniku zastosowania środka ochronnego o skuteczności A do maszyny z ryzykiem wyjściowym Rr, ryzyko rzeczywiste wynosi:

Ra = Rr – A = S + F + P – A.

ciężkość

Wprowadzamy dodatkową wartość S0 = 0.

S	ciężkość
0	drobne: stłuczenia, skaleczenia, oparzenia I stopnia
1	odwracalne: złamania, przecięcia, oparzenia II stopnia
3	nieodwracalne: zmiażdżenia, amputacje, oparzenia III stopnia, zeszpecenie, śmierć

częstość

Norma określa F2 jako częściej niż raz na 15 minut.

Dodatkowo należy uwzględnić, że najniższy poziom niezawodności odpowiada częstości raz na rok (10.000 godzin). Norma mówi też, że dla zdarzeń mało prawdopodobnych można obniżyć PLr o jeden poziom, co odpowiada ok. dziesięciokrotnemu wzrostowi prawdopodobieństwa awarii. Dla bardzo rzadkich zdarzeń można więc wprowadzić dodatkową wartość F0 = 0.

F	częstość
0	rzadko: rzadziej niż raz na tydzień13)ok. 1000 razy rzadziej niż F2
1	często: raz na 15 minut lub rzadziej
2	stale: częściej niż raz na 15 minut

możliwość uniknięcia

P	możliwość uniknięcia zagrożenia lub ograniczenia szkody
0	istnieje rzeczywista szansa uniknięcia zagrożenia
1	uniknięcie zagrożenia jest prawie niemożliwe14)tak dosłownie określa to norma, choć powinno być raczej: „trudne“